The Building Phylogenetic Tree dialog for the PHYLIP Neighbour-Joining method has the following view:
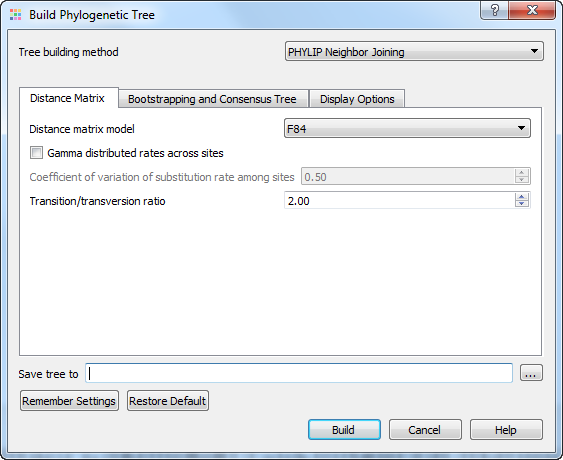
The following parameters are available:
Distance matrix model — model to compute a distance matrix. The following values are available for a nucleotide multiple sequence alignment:
- F84
- Kimura
- Jukes-Cantor
- LogDet
The following models are available for a protein alignment:
- Jones-Taylor-Thornton
- Henikoff/Tillier PMB
- Dayhoff PAM
- Kimura
Gamma distributed rates across sites — specifies to take into account unequal rates of change at different sites. It is assumed that the distribution of the rates follows the Gamma distribution.
Coefficient of variation of substitution rate among sites — becomes available if the Gamma distributed rates across sites parameter is checked. Specifies the coefficient of the distribution of the rates.
Transition/transversion ratio — expected ratio of transitions to transversions.
To enable bootstrapping check the Bootstrapping and Consensus Trees group check box. The following parameters are available:
Number of replicates — number of replicate date sets.
Seed — random number seed. By default, it is generated automatically. You can manually change this value in order to make results of different runs (of a tree building) reproducible. The should must be an integer greater than zero and less than 32767 and which is of the form 4n+1, that is, it leaves a remainder of 1 when divided by 4. Any odd number can also be used, but may result in a random number sequence that repeats itself after less than the full one billion numbers. Usually this is not a problem.
Consensus type — specifies the method to build the consensus tree. Select one of the following:
- Strict — specifies that a set of species must appear in all input trees to be included in the strict consensus tree.
- Majority Rule (extended) — specifies that any set of species that appears in more than 50% of the trees is included. The program then considers the other sets of species in order of the frequency with which they have appeared, adding to the consensus tree any which are compatible with it until the tree is fully resolved. This is the default setting.
- M1 — includes in the consensus tree any sets of species that occur among the input trees more than a specified fraction of the time (see the Fraction parameter below). The Strict consensus and the Majority Rule consensus are extreme cases of the Ml consensus, being for fractions of 1 and 0.5 respectively.
- Majority Rule — specifies that a set of species is included in the consensus tree if it is present in more than half of the input trees.
Fraction — becomes available when the Consensus type parameter is set to M1. Specifies the fraction.
Display tree in new window - displays tree in new window.
Display tree with alignment editor - displays tree with alignment editor.
Synchronize alignment with tree - synchronize alignment and tree.
Save tree to — file to save the tree built.
Press the Build button to build a tree with the parameters selected.